Éditions Hatier, Paris, 2023
quiz

Quiz du chapitre 1

Pour chaque question, cochez la ou les réponse(s) exacte(s) :

  1. 1. (un) est une suite arithmétique de premier terme u0 = – 2 et de raison r = 3. Alors, u4 est égal à :

    003x
    • 7.
    • 12.
    • 10.
    • 14.

  2. 2. (un) est une suite arithmétique telle que : u1 = – 5 et u2 = 2. Alors la raison r est égale à :

    001x
    • 7.
    • –3.
    • – 5.
    • – 7.

  3. 3. (un) est une suite arithmétique de premier terme u0 = 3 et de raison r = –1.

    Sn = u0 + u1 + … + un. Alors, S5 égale à :

    002x
    • 5.
    • 3.
    • 2.
    • 0.

  4. 4. (un) est une suite arithmétique de raison – 5. Laquelle des affirmations suivantes est exacte ?

    003x
    • Pour tout entier n, un+1 − un = 5.
    • u10 = u2 + 40.
    • u3 = u7 + 20.
    • u2u1\frac{u_{2}}{u_{1}} = 5.

  5. 5. (un) est une suite géométrique de premier terme u0 = 3 et de raison q = 4. Alors (u3) est égal à :

    004x
    • 12.
    • 48.
    • 64.
    • 192.

  6. 6. (un) est une suite géométrique de premier terme u0 = 3 et de raison q = 2.

    Sn = u0 + u1 + … + un.

    Alors, S10 est égal à :

    003x
    • 1 024.
    • 3 069
    • 6 144
    • 7 168

  7. 7. On place un capitale C0 = 1 000 € sur un livret bancaire rémunéré à 1 %, avec intérêts annuels composés. Cela signifie que, chaque année, on perçoit des intérêts d'un montant égal à 1 % du capital qui s'ajoutent alors au capital. Au bout d'un an, le capital disponible est :

    C1 = 1 000 × 1,01 = 1 010 €, puis au bout de deux ans, C2 = 1 010 × 1,01 = 1 020,1 €.

    On désigne par C0, C2, …, Cn les capitaux disponibles (ou "valeurs acquises") au bout de 1,2 … n années.

    C2, …, Cn sont des termes successifs d'une suite géométrie de raison :

    004x
    • 1.
    • 0,1.
    • 0,01.
    • 1,01.

  8. 8. On reprend le placement du 7. Au bout de cinq ans, le capital disponible est égal à :

    003x
    • 1 050.
    • 1 051,01.
    • 1 040,60.
    • 1 062.

  9. 9. On décide d'utiliser une feuille de calcul pour déterminer les termes d'une suite géométrique de premier terme u0 = 120 et de raison q = 0,75.

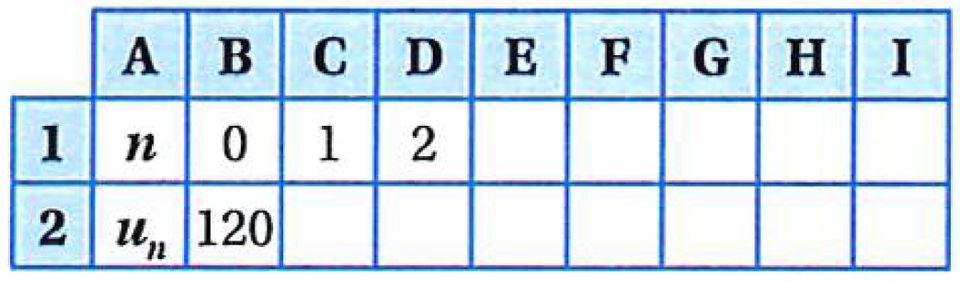
    16999_C1_tableau

    Quelle formule doit-on entrer en C2 et recopier vers la droite ?

    003x
    • =$B2*0,75 ;
    • =$B2*0,75^C1 ;
    • =$B2*0,75$C1 ;
    • =B2*0,75 ;

  10. 10. On considère la suite définie par u0 = 5 et, pour tout entier naturel n, un+1 = un × 0,8. La valeur de la variable u après avoir exécuté les instructions suivantes :

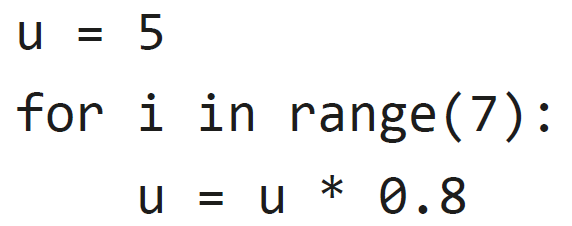
    C1_tableau3

    est :

    003x
    • 1,638 4.
    • 1,310 72.
    • 1,048 576.
    • 0,838 860 8.
Score : 10 1