A. 1. (u_n) est une suite arithmétique de premier terme u₀ = – 2 et de raison r = 3. Alors, u₄ est égal à :

2. (u_n) est une suite arithmétique telle que : u₁ = – 5 et u₂ = 2. Alors la raison r est égale à :

3. (u_n) est une suite arithmétique de premier terme u₀ = 3 et de raison r = –1.

S_n = u₀ + u₁ + … + u_n. Alors, S₅ égale à :

4. (u_n) est une suite géométrique de premier terme u₀ = 3 et de raison q = 4. Alors u₃ est égal à :

5. (u_n) est une suite géométrique de premier terme u₀ = 3 et de raison q = 2.

S_n = u₀ + u₁ + … + u_n. Alors, S₁₀ égale à :

6. La production d'une entreprise du secteur des énergies renouvelables augmente de 10 % chaque année. Au bout de 4 ans, elle aura augmenté d'environ :

B. L'iode 131 est un produit radioactif. La masse de tout échantillon d'iode 131 diminue régulièrement de 8,3 % par jour par

désintégration. On dispose d'un échantillon de masse initiale M₀ = 100 g. On note M_n la masse de cet échantillon au bout de n jours.

1. Arrondie au dixième, la masse M₂ de l'échantillon au bout de 2 jours est :

2. La suite des nombres M_n est une suite :

3. On veut calculer les masses successives de l'échantillon à l'aide d'un tableur.

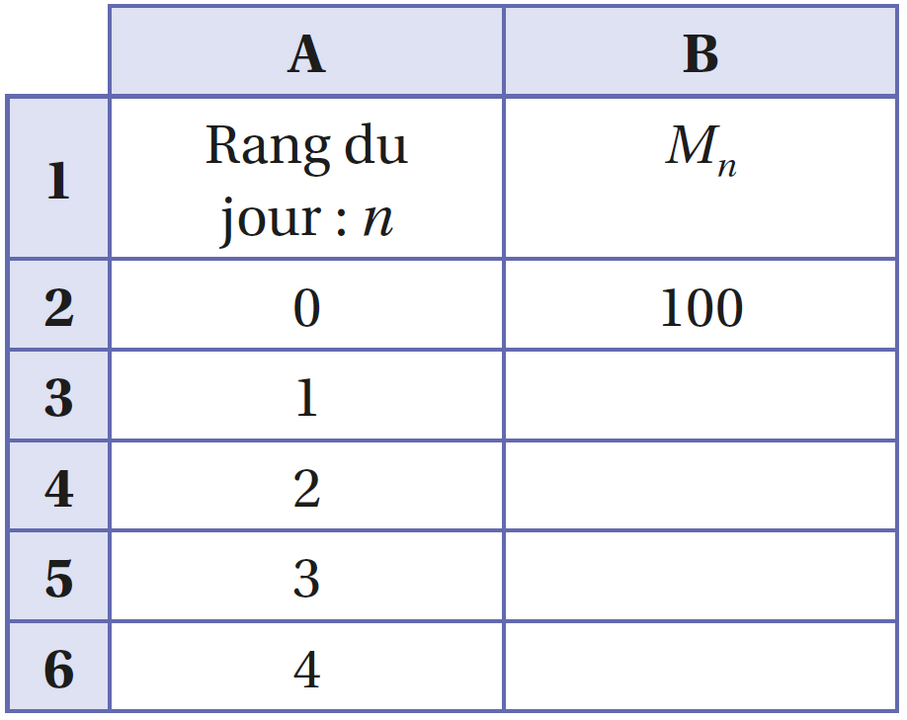
La formule à écrire en B3 pour obtenir, en la recopiant vers le bas, les termes M de la suite dans la colonne B, est :

4. La masse de l'échantillon est inférieure à 10 grammes au bout de :

5. On considère la suite définie par u₀ = 5 et, pour tout entier naturel n, u_n+1 = u_n × 0,8. La valeur de la variable u après avoir exécuté les instructions suivantes :

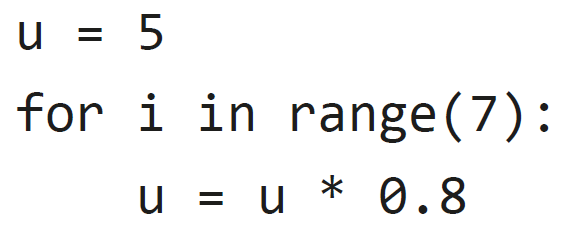
est :