A. Le tableau ci-dessous donne des informations concernant les pratiques artistiques et sportives de 400 élèves d'un lycée.

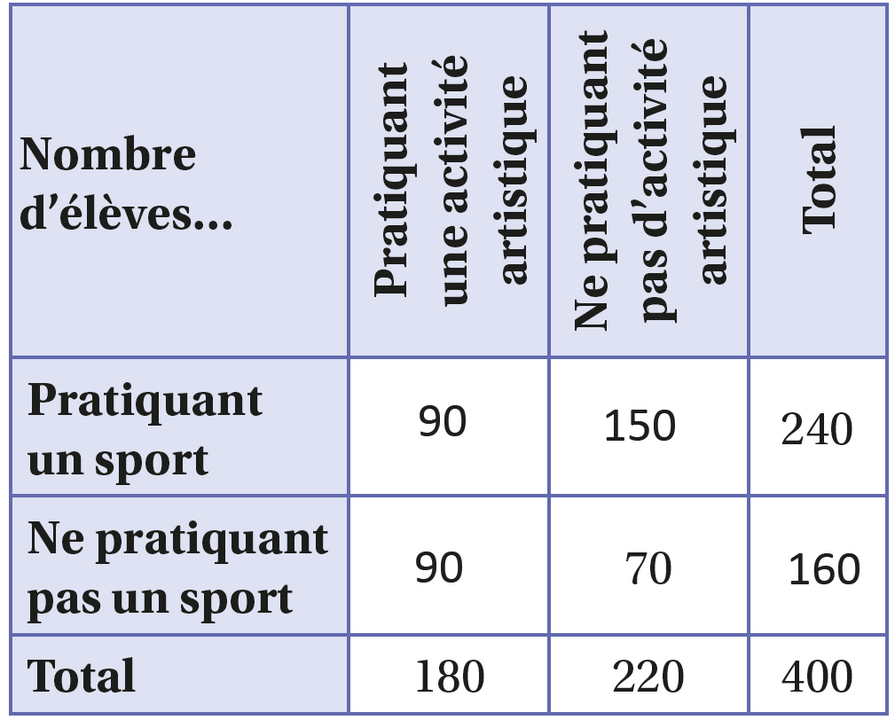
On choisit un élève de ce lycée au hasard. Tous les élèves ont la même probabilité d'être choisis. On définit les événements suivants :

A : « l'élève choisi pratique une activité artistique » ;

S : « l'élève choisi pratique un sport ».

1. La probabilité que l'élève choisi pratique un sport et une activité artistique est :

2. Sachant qu'un élève pratique un sport, la probabilité qu'il pratique une activité artistique est :

3. La probabilité qu'un élève de ce lycée choisi au hasard pratique un sport ou une activité artistique est :

4. La probabilité P_A(S) est égale à :

B. Une maladie virale atteint 0,5 % d'une population. Un dépistage systématique est mis en place à l'aide d'un test.

On admet que :

• quand une personne est malade, le test est positif dans 80 % des cas ;

• quand une personne n'est pas malade, le test est négatif dans 90 % des cas.

On choisit une personne au hasard dans cette population, toutes les personnes ayant la même probabilité d'être choisies.

On considère les événements suivants :

M : « la personne choisie est malade » ;

T : « la personne choisie a un test positif ».

On donne l'arbre pondéré suivant.

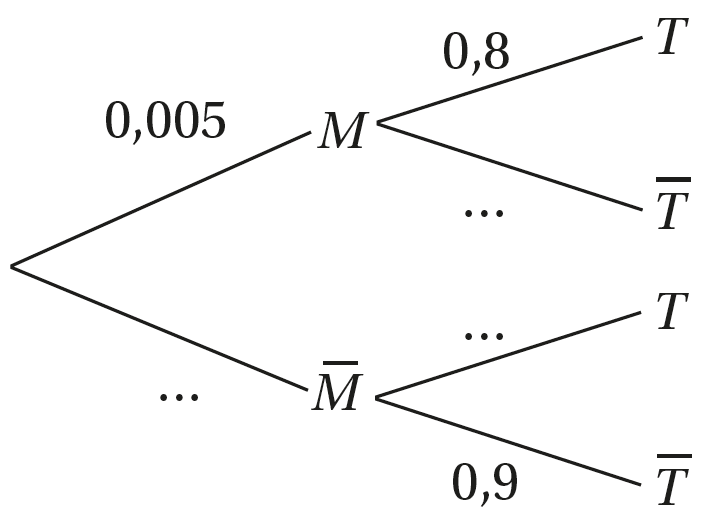
1. La probabilité que la personne choisie ne soit pas malade est :

2. P_M($\bar{T}$) =

3. La probabilité que la personne choisie soit malade avec un test négatif est :

4. P(T)=

5. La meilleure approximation de P_T(M) est :

C. La loi de probabilité d'une variable aléatoire X est définie par :

1. L'espérance de X est :

2. X est une variable aléatoire qui à chaque partie d'un jeu associe le gain en euros du joueur. Le jeu est équitable.

D. La variable aléatoire X suit la loi binomiale de paramètres n = 7 et p = 0,03.

Dans ce qui suit, les résultats proposés sont des valeurs approchées arrondies à 10^–3.

1. La probabilité P(X = 0) est égale à :

2. La probabilité P(X ≤ 1) est égale à :